マトリックスを使った座標の計算
まずは、このマトリックスでどうやって座標の計算をするかですが
点 P (x , y , z , 1.0) をマトリックスで変換した点 P' (x' , y' ,
z ', 1.0) は次のように求めます

ということになります
3次元の点なのに、1.0って何者なのか?
よく解からんのですが、これは、AutoCADで変換マトリックス使う場合のお約束だそうです (^^ゞ
それから nentsel が返すマトリックスだけ
4行3列 なので注意しましょう
nentselp は4行4列のマトリックスを返しますので、こちらを使ったほうが便利です
この、マトリックス(4行4列)は、リストであらわすと
( (m00 m01 m02 m03)
(m10 m11 m12 m13)
(m20 m21 m22 m23)
( 0.0 0.0 0.0 1.0 ) )
となります
最後の行 (0.0 0.0 0.0 1.0)
これもお約束なのであります (-_-;)
また、この計算をLispで書くと
;************************************************************************************; ;マトリックス変換 ; (defun Jof_trans_mat( mat;変換マトリックス 4X4; pt ;変換する3Dポイント(x y z); ) (setq pt (append pt '(1.0))) (reverse (cdr (reverse (mapcar '(lambda (x) (apply '+ (mapcar '* pt x))) mat)))) )となります
ためしに計算してみましょう
コマンド: (load "Jof_trans_mat") JOF_TRANS_MAT コマンド: (setq mat '((1 0 0 3)(0 1 0 2)(0 0 1 0)(0 0 0 1))) ((1 0 0 3) (0 1 0 2) (0 0 1 0) (0 0 0 1)) コマンド: (setq pt '(0 0 0)) (0 0 0) コマンド: (jof_trans_mat mat pt) (3.0 2.0 0.0)(0 0 0) は (3.0 2.0 0.0)に変換されました
続いて、このマトリックスが何を表しているのかについてみてみましょう
恒等のマトリックス(なにも変化しないやつ)
( (1.0 0.0 0.0 0.0)
(0.0 1.0 0.0 0.0)
(0.0 0.0 1.0 0.0)
(0.0 0.0 0.0 1.0) )
ほらね
コマンド: (setq mat '((1 0 0 0)(0 1 0 0)(0 0 1 0)(0 0 0 1)))
((1 0 0 0) (0 1 0 0) (0 0 1 0) (0 0 0 1))
コマンド: (setq pt '(1 2 3))
(1 2 3)
コマンド: (jof_trans_mat mat pt)
(1.0 2.0 3.0)
移動を表すマトリックス
( (1.0 0.0 0.0 x )
(0.0 1.0 0.0 y )
(0.0 0.0 1.0 z )
(0.0 0.0 0.0 1.0) )
ためしてみましょう
x方向に5、y方向に5移動してみましょう
マトリックスは
( (1.0 0.0 0.0 5.0)
(0.0 1.0 0.0 5.0 )
(0.0 0.0 1.0 0.0 )
(0.0 0.0 0.0 1.0) )
コマンド: (setq mat '((1 0 0 5)(0 1 0 5)(0 0 1 0)(0 0 0 1)))
((1 0 0 5) (0 1 0 5) (0 0 1 0) (0 0 0 1))
コマンド: (setq pt '(3 2 0))
(3 2 0)
コマンド: (jof_trans_mat mat pt)
(8.0 7.0 0.0)
尺度を表すマトリックス
(WCS原点を基点に尺度を変更するマトリックス)
( ( x 0.0 0.0 0.0 )
(0.0 y 0.0 0.0 )
(0.0 0.0 z 0.0 )
(0.0 0.0 0.0 1.0) )
Z軸回転を表すマトリックス
(Z軸まわり(x-y平面)でWCS原点を中心にθ
回転するマトリックス)
( (cosθ -sinθ 0.0 0.0 )
( sinθ cosθ 0.0 0.0 )
(0.0
0.0 1.0 0.0 )
(0.0
0.0 0.0 1.0) )
これもためしてみます
θ=30°とすると
cosθ=0.866025 sinθ=0.5となりますね
ですから、マトリックスは
( (0.866025 -0.5
0.0 0.0 )
(0.5 0.866025 0.0 0.0 )
(0.0
0.0 1.0 0.0 )
(0.0
0.0 0.0 1.0 ) )
コマンド: (setq mat '((0.866025 -0.5 0 0)(0.5 0.866025 0 0)(0 0 1 0)(0 0 0 1)))
((0.866025 -0.5 0 0) (0.5 0.866025 0 0) (0 0 1 0) (0 0 0 1))
コマンド: (setq pt '(3 2 0))
(3 2 0)
コマンド: (jof_trans_mat mat pt)
(1.59808 3.23205 0.0)
X軸回転を表すマトリックス
(X軸まわり(y-z平面)でWCS原点を中心にθrad
回転するマトリックス)
( (1.0
0.0 0.0 0.0 )
(0.0 cosθ -sinθ 0.0 )
(0.0 sinθ cosθ 0.0 )
(0.0 0.0
0.0 1.0 ) )
Y軸回転を表すマトリックス
(Y軸まわり(x-z平面)でWCS原点を中心にθrad
回転するマトリックス)
( (cosθ 0.0 sinθ
0.0 )
(0.0
1.0 0.0 0.0 )
(-sinθ 0.0 cosθ 0.0 )
(0.0
0.0 0.0 1.0) )
マトリックスの表すもの
移動のマトリックスで検証したものを図で表してみました
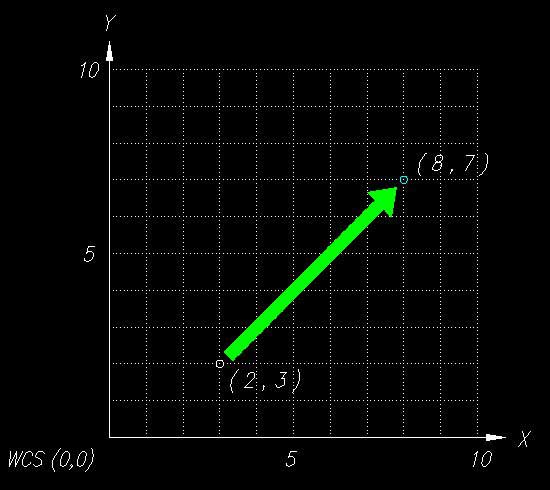
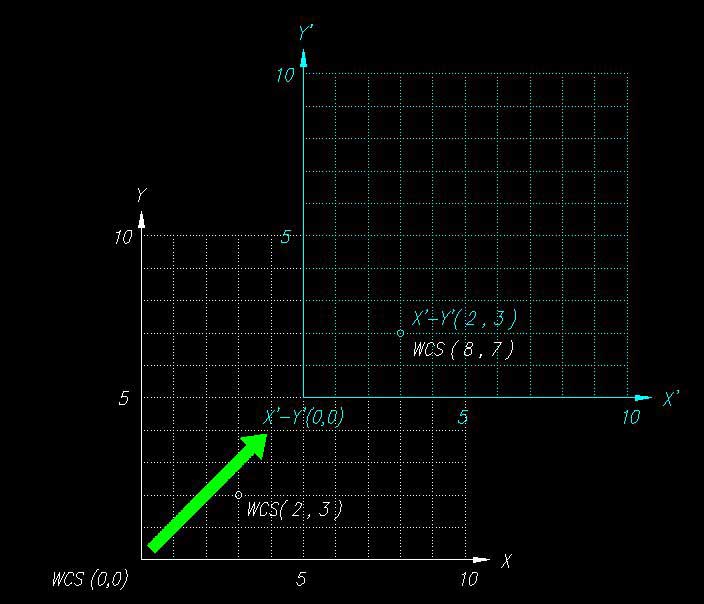
これは、別の見方をすると・・・・
WCS (3 , 2 , 0) の点を、原点を WCS (5 , 5 , 0)
とする新しい座標系X'-Y' において、X'-Y'(3 , 2 , 0) が示す点は
WCS (8 , 7 , 0) であるということです
新しい座標系X'-Y' をUCSと考えると理解しやすいかもしれません
だから、座標変換とか言うわけですね (^^ゞ
同様に回転のマトリックスも、原点 WCS (0 , 0 , 0) を中心に回転させた、新しい座標系X'-Y' で X'-Y'(3 , 2 , 0) が示す点を計算していると考えてもいいわけです
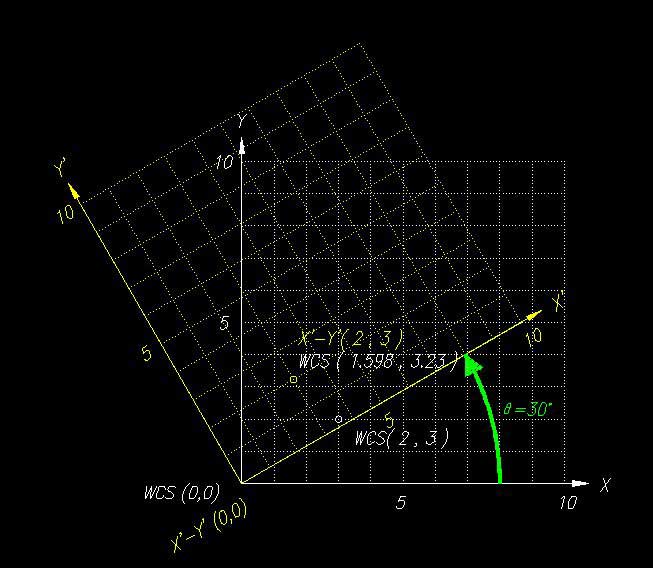
では、ためしに、実際に新しい座標系X'-Y'をUCSとして設定してみましょう
まずは移動のマトリックスで変換される座標系をUCSに設定します
そして、システム変数 UCSXDIR UCSYDIR UCSORG を調べてみると
コマンド: UCSXDIR
UCSXDIR = 1.0000,0.0000,0.0000 (読み込み専用)
コマンド: UCSYDIR
UCSYDIR = 0.0000,1.0000,0.0000 (読み込み専用)
コマンド: UCSORG
UCSORG = 5.0000,5.0000,0.0000 (読み込み専用)
続いて回転のマトリックスで変換される座標系をUCSに設定します
そして、システム変数 UCSXDIR UCSYDIR UCSORG を調べてみると
コマンド: UCSXDIR
UCSXDIR = 0.8660,0.5000,0.0000 (読み込み専用)
コマンド: UCSYDIR
UCSYDIR = -0.5000,0.8660,0.0000 (読み込み専用)
コマンド: UCSORG
UCSORG = 0.0000,0.0000,0.0000 (読み込み専用)
この数字見覚えありませんか?
そう、UCSXDIRの値は 変換マトリックスの1列目
UCSYDIRの値は 変換マトリックスの2列目
UCSORGの値は 変換マトリックスの4列目なんです
CAD上では尺度の違う座標系をUCSに設定できないので試せませんが、つまりこうゆうこと

マトリックスは、まさに、変換先の座標系を表していたのです
尺度は、それぞれのベクトルの長さで表されます
長くなったので、ひとまずここまで <(_ _)>
その2に続く